Backpropagation

Phần backpropagation này rất nặng về toán đạo hàm nhé. Nên ai chưa có kiến thức đạo hàm riêng thì bắt buộc phải học trước đi nhé.

Ý nghĩa của đạo hàm riêng

Giả sử ta có hàm f = xy. Theo đạo hàm riêng thì ta có:

$\frac{\delta f}{\delta x}=y$ , $\frac{\delta f}{\delta y}=x$

Ví dụ với x= 4 và y =-3. Quá trình forward là quá trình tính toán theo biểu thức để ra kết quả. Tức forward ở đây là 4.-3 = -12. Lúc này, ta có đạo hàm riêng theo x = -3. Điều này có nghĩa là, nếu ta tăng giá trị của x 1 khoảng h nào đó, thì toàn bộ hàm f sẽ giảm một khoảng là -3h. Tương tự với đạo hàm riêng theo y = 4. Điều này có nghĩa, nếu ta tăng giá trị y 1 khoảng h nào đó, thì toàn bộ giá trị của f sẽ tăng 1 khoảng 4h. Như vậy, có thể hiểu:

Đạo hàm riêng của 1 biến chỉ ra được sự ảnh hướng của biến đó tới sự biến động của toàn bộ hàm số.

Các ví dụ

Giả sử ta có biểu thức: f(x,y,z)=(x+y)z. Giả sử x = -2, y = 5, z = -4. Ta có thể vẽ biểu thức như sau: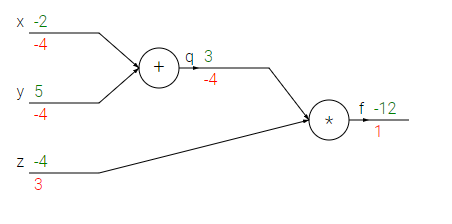

Còn quá trình backpropagation là quá trình tính đạo hàm của từng thành phần bằng cách tính ngược từ kết quả lên. Có thể thấy: q = x+ y có đạo hàm riêng là -4. Do đó, ta có thể nói rằng: nếu x hay y tăng thì q sẽ tăng, và f sẽ giảm 1 khoảng 4 lần giá trị tăng.  
Ví dụ tiếp theo cho hàm sigmoid Giả sử ta có hàm sau (gọi là hàm sigmoid):

$f(x,y)=\frac{1}{1+e^{-(w_{0}x_{0}+w_{1}x_{1}+w_{2})}}$

Ta có thể biểu diễn nó ra được như hình sau: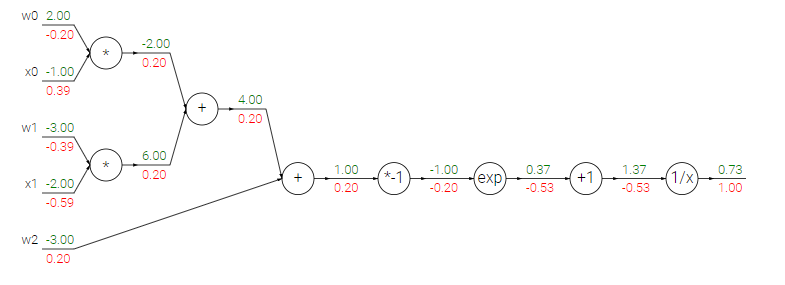

Quá trình tính toán forward cực kì đơn giản, bạn có thể tự tính ra được như trong hình. Mình sẽ giải thích quá trình backpropagation cho trường hợp này:
Giả sử cho kết quả output có đạo hàm = 1 cho dễ tính. Ta backward 1 bước về phép tính 1/x. Đạo hàm riêng của 1/x = -1/x^2 . Do đó ta có kết quả đạo hàm riêng tại đây là : (-1/1.37^2)*1 = -0.53. Tiếp đến ta backward 1 bước về phép tính x +1 . Đạo hàm theo x = 1. Do đó kết quả đạo hàm riêng tại đây = 1*-0.53 = -0.53. Tiếp tục backward lại 1 bước về phép tính :e^x . Ta có đạo hàm theo x của e^x = e^x. Do đó, đạo hàm riêng của x tại đây = e^-1*-0.53 = -0.2. Cứ thế, ta tính ngược cho đến input. Quá trình này chính là quá trình backpropagation.

Backpropagation và gradient descent

Quay lại với hàm score function, ta có $f(x_{i},W)=Wx_{i}$, loss function(SVM loss) $L_{i}=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+\Delta )$. Giả sử W là tập hợp của 1 trăm triệu weight từ W1 đến W100 triệu. Và qua quá trình backpropagation của hàm L, ta có đạo hàm riêng của $\frac{\delta L}{\delta W_{69}}=-4$. Điều này có ý nghĩa là: Nếu W69 tăng 1 khoảng h, thì L sẽ giảm 1 khoảng -4h. Đúng chưa nào? Mục tiêu chúng ta đặt ra từ đầu là làm cho L giảm (loss càng thấp thì dự đoán càng chính xác).
Tiếp tục ôn bài gradient descent nè: để L giảm thì ta xài gradient descent với công thức $W_{t+1} = W_{t}-\alpha f'(W_{t})$. Với $\alpha > 0$. Áp vào cho W69, ta có : $W'_{69} = W_{69} - \alpha(-4)$. Tức là W69 sẽ tăng sau vòng lặp này, đồng nghĩa là L sẽ giảm sau vòng lặp này.
 Và bây giờ, hiệu ứng quá rõ ràng: nhờ backpropagation tính ra đạo hàm riêng cho W, mà ở bước lặp tiếp theo, W sẽ thay đổi dựa vào gradient descent. Và sự thay đổi này làm L ở vòng lặp tiếp theo giảm. Tức là sự dự đoán ở vòng lặp tiếp theo sẽ chính xác hơn!