Score function là một hàm có khả năng chuyển từng pixel trên 1 bức ảnh thành các điểm tin cậy (confidence score) tương ứng với mỗi nhãn dán.
Đọc khái niệm thì có vẻ khó hiểu. Nhưng cứ đi vào ví dụ thì mọi chuyện sẽ dễ dàng hơn.
Giả sử ta có 1 tập training set gồm i bức hình $x_{i}\epsilon R^{D}$, mỗi bức hình có nhãn dán tương ứng là $y_{i}$. Trong đó i ∈ 1..N và $y_{i}$ ∈ 1..K . Tức là, chúng ta có 1 tập N bức hình (D chiều) và K nhãn dán phân loại.
Ví dụ dễ hiểu: với tập CIFAR-10 ta có N = 50000 , D = 32*32*3 = 3072 điểm ảnh, K =10 nhãn dán.
Vậy score function lúc này là 1 hàm sexcos khả năng chuyển các điểm ảnh $R^{D}$ về thành các điểm tương ứng với nhãn dán $R^{K}$
$f:R^{D}$↦$R^{K}$
Linear Classifier (Hàm tuyến tính)
Linear classifier là hàm cơ bản nhất (theo mình nghĩ), nó được viết như sau:
$f(x_{i},W,b)=Wx_{i}+b$
Với công thức trên, giả sử ta duỗi thẳng các pixels của 1 bức hình thành 1 vector duy nhất [D*1]. Ma trận W sẽ có kích thước là [K*D], vector b có kích thước là [K*1]. W và b này là các parameters của hàm. Ví dụ trong cifar-10, $x_{i}$ chứa tất cả pixels của bức hình thứ I, được duỗi thẳng ra thành 1 vector [3072*1] , W = [10*3072], b = [10*1]. Vậy với hàm trên, đầu vào sẽ là 3072 con số, và đầu ra sẽ là 10 con số.
Nhìn lại định nghĩa của Score function dùm mình: Score function nhận đầu vào là 1 bức hình (thực chất là $x_{i}$ ), đầu ra là confidence score tương ứng với nhãn dán ( hàm $f(x_{i},W,b)=Wx_{i}+b$ cho đầu ra là một vector 10 con số với trường hợp là tập Cifar-10).
Cũng nhắc luôn, W là weights, b là bias. Nhưng mình thường gọi chung hết W và b là parameters.
Ví dụ cho linear classifier

Ghép chung W và b trong toán học
Theo như công thức linear classifier ở trên, chúng ta đã tách biệt W và b. Nhưng thông thường khi lập trình và tính toán, người ta có thể gộp chung 2 phần tử trên thành 1 ma trận chung.
$f(x_{i},W)=Wx_{i}$
Việc gộp này thực hiện như thế nào, bạn nhìn vào hình sau sẽ rõ: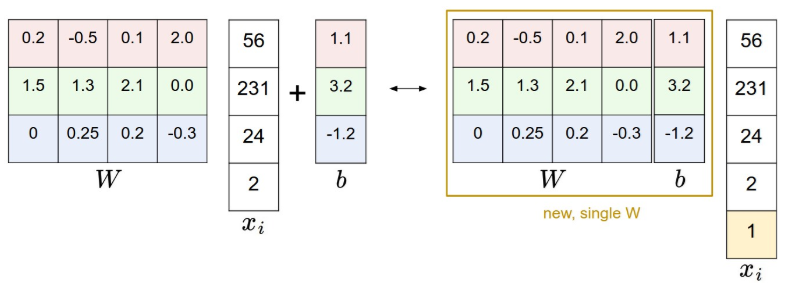

0 nhận xét:
Đăng nhận xét