Image Classification

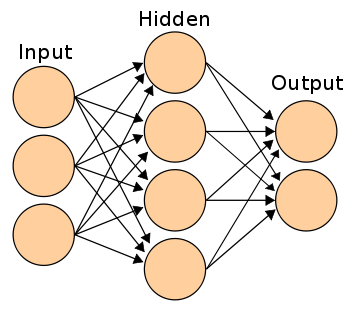
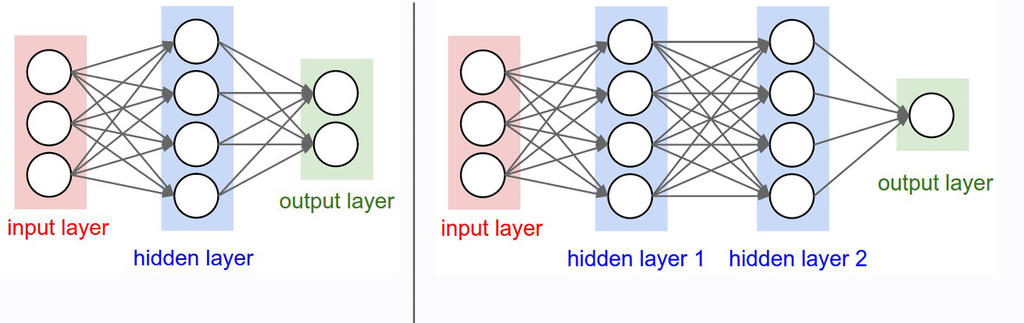
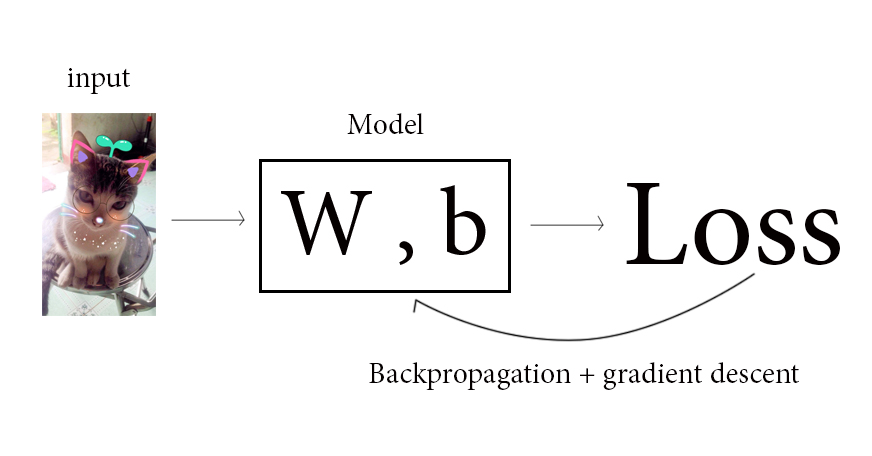
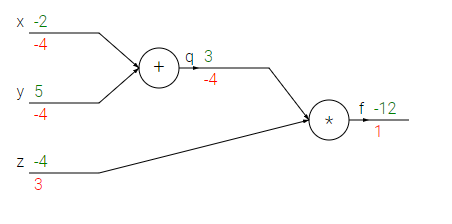
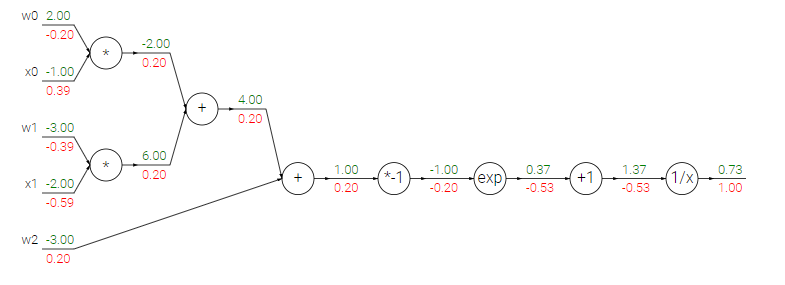
Chào mừng bạn đến với các bài học Image classification, một trong những bài học thuộc mảng Computer Vision được mình viết trên blog cá nhân. Mong rằng qua những bài học trong series này, bạn sẽ nắm vững được một số kiến thức cơ bản trong việc phân loại hình ảnh sử dụng các phương pháp máy học, để từ đó có thể làm tiền đề cho những ứng dụng sau này của bản thân.
Bài 1 : Giới thiệu
Bài đầu tiên sẽ giới thiệu tổng quan về series image classification.
Bài 2 : Image classification
Bài này sẽ giới thiệu tổng quan về image classification
Bài 3 : Thuật toán Nearest Neighbor Classifier
Thuật toán phân lớp Người láng giềng gần nhất
Bài 4 : Cài đặt Nearest Neighbor Classifier với ngôn ngữ Python
Bài 5 : Thuật giải K-Nearest Neighbor
Bài 6 : Cài đặt K-Nearest Neighbor Classifier với ngôn ngữ Python
 Bắt đầu từ đây, các bài tiếp theo sẽ dính dáng khá nhiều tới toán học nhé mấy man. Nếu không hiểu công thức toán thì cứ kệ đi nhá :v Vì biết đâu đọc ví dụ lại hiểu. Đó cũng là cách mình đọc tài liệu ( vì mình không giỏi toán lắm).
Bài 7 : Score function
Bài 8 : Loss function
Bài 9: Optimization và Gradient Descent
Bài 10: Backpropagation
Bài 11: Giải thích quá trình máy học
Như vậy, chúng ta đã hiểu máy học là gì. Những phần tiếp theo, chúng ta sẽ tìm hiểu về model. Những model được đem vào mổ sẻ là ANN (mạng nơ ron nhân tạo) và CNN (mạng nơ ron tích chập).
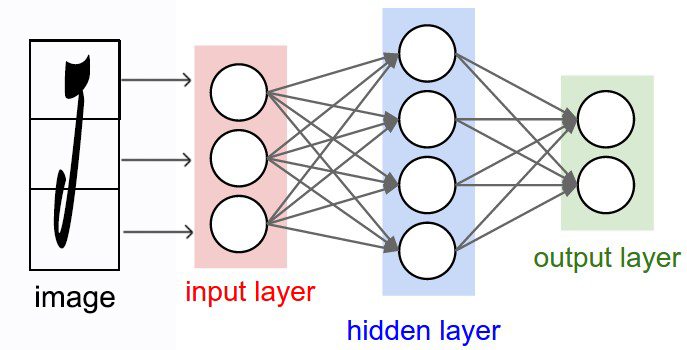
Bài 12: Kiến trúc mạng neural nhân tạo
Bài 13: Cấu trúc của 1 neural
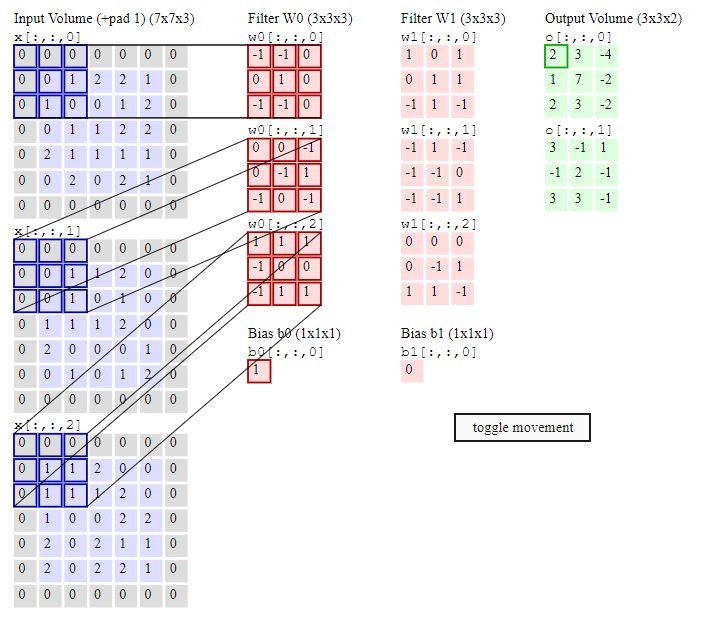
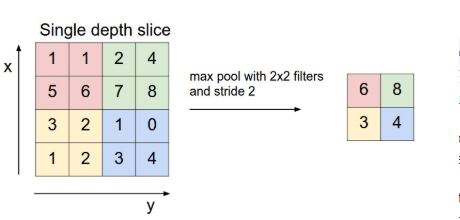
Bài 14: Tìm hiểu mạng CNN
 Okie, Vậy là chúng ta đã hoàn thành được bài CNN, cũng là bài cuối trong loạt series image classification của mình. Đây chỉ là kiến thức nền cơ bản để các bạn hiểu và nắm được các khái niệm của Classification và những mạng model dùng để giải quyết bài toán đó. Mong các bạn dựa vào đây có thể tự mình tìm hiểu và phát huy được bản thân trong lĩnh vực đầy thú vị này. Chào thân ái và quyết thắng.

Read More

Tìm hiểu về Convolutional Neural Network (CNN)

Chúng ta đã được tìm hiểu về mạng neural nhân tạo trong bài này. Nếu như đầu vào của chúng ta là 1 bức hình 30*30*3 pixel, thì lớp input của neural network sẽ là 30*30*3 neural. Số lượng neural này vẫn tạm chấp nhận được cho quá trình training vì chi phí tính toán cũng chưa phải là lớn lắm. Nhưng nếu đầu vào của chúng ta là bức hình 1000*1000*3, thì số lượng neural lúc này cực kì lớn và quá trình tính toán sẽ chậm đi rất nhiều, đồng thời mạng phức tạp sẽ dễ dẫn đến overfitting.
Mặt khác, với đối tượng đầu vào là bức hình, thì các pixel gần nhau hợp lại sẽ mang những thông tin hữu ích, nhưng neural network thì không khai thác được đặc điểm này. Do đó, có một mạng neural mới, được người ta nghiên cứu sáng tạo ra: đó là convolutional neural network (CNN). Vậy CNN khác với ANN như thế nào? Hiểu một cách nôm na thì CNN không đọc từng pixel riêng lẻ như ANN, mà nó sẽ đọc 1 loạt các pixel gần nhau để đưa vào tính toán. Nhưng để hiểu rõ hơn về cách hoạt động của CNN, chúng ta phải đi vào tìm hiểu từng thành phần cấu tạo nên mạng CNN mới rõ đc. Ở đây chúng ta sẽ tìm hiểu các khái niệm mới như Convolutional Layer, Pooling Layer.

Convolutional Layer:

Convolutional Layer là 1 lớp cực kì quan trọng trong CNN, nó đảm nhận hầu hết chức năng tính toán của mạng.

Để giải thích về Convolutional Layer, mình sẽ đi thẳng trực tiếp vào ví dụ để giải thích cho trực quan.
Đầu tiên là khái niệm filter map: thay vì kết nối với từng pixel của hình ảnh đầu vào như ANN, CNN có những tấm filter dùng để áp vào những vùng của bức hình. Các filter map này thực chất là một ma trận 3 chiều gồm các con số. Và điều bạn cần phải cực kì lưu ý là các con số này chính là các parameter cần phải học. Filter map có kích thước dài và rộng là hyperparameter ( hyperparameter là gì thì mình có nói trong bài này) , riêng chiều cao ( mình sẽ gọi là depth - chiều sâu ) của filter map sẽ bằng với depth của lớp trước.
Ví dụ nhìn vào hình ví dụ ở trên, chúng ta có 2 filter map màu hồng là W0 và W1. Mỗi filter map có kích thước 3*3*3. Kích thước dài * rộng ( 3*3 ) là hyperparameter, còn chiều sâu (Depth) sẽ bằng với depth của input volumn, tức là bằng 3.
Stride: như đã nói ở trên, filter map được dùng để trượt lên tấm hình đầu vào, vậy trượt ở đây có nghĩa là như thế nào? Rất đơn giản, chỉ cần dịch filter map theo pixel từ trái sang phải theo từng dòng. Mỗi lần dịch như thế sẽ dựa vào 1 giá trị gọi là stride.
Ví dụ, stride = 1, thì mỗi lần dịch filter map sẽ sang phải 1 pixel, khi hết cạnh biên phải thì xuống 1 dòng và dịch tiếp. Còn nếu stride = 2 thì mỗi lần dịch sẽ sang phải 2 pixel, khi hết cạnh thì xuống 2 dòng.  
Padding: người ta sẽ thêm những giá trị 0 bao quanh lớp input. Ví dụ như ở trên hình, lớp input của chúng ta ban đầu có kích thước 5*5*3, nhưng vì giá trị padding = 1, nên được bao thêm 1 lớp 0 bên ngoài. Từ đó, kích thước của lớp input = 7*7*3.
Feature map: feature map thực chất là kết quả sau khi lớp input được filter map quét qua hết. Với mỗi lần filter map áp lên input, sẽ có quá trình tính toán xảy ra. Vậy quá trình tính toán này là gì? Thực chất đó là quá trình nhân 2 ma trận.
Ví dụ như trên hình, khi lớp trên cùng của filter map W0 áp vào lớp trên cùng của input volum, ma trận filtermap w0 3*3 sẽ được nhân với ma trận 3*3 của input sau đó cộng thêm bias=1, và đưa ra kết quả = 2 ở feature map. Kích thước feature map được tính như nào? Mỗi lần 1 filter map trượt hết lên input volum sẽ cho ra 1 lớp của feature map. Vậy nên, depth của feature map sẽ bằng số lượng filter map.
Ví dụ như hình trên, depth của feature map = số lượng filter map = 2. Còn chiều dài và chiều rộng của feature map sẽ được tính bằng công thức: (W + 2P - F)/S +1 . Trong đó, W là kích thước input, P là padding, F là kích thước filter map, S là stride.
Ví dụ với hình, W = 5, P =1, F = 3, S =1 , ta tính được kích thước của feature map là 3.
Ta có thể thấy được, nếu với ANN thông thường, 1 bức hình 7*7*3 như trên sẽ cần có 7*7*3 = 147 parameters (nếu lớp thứ 2 chỉ có 1 neural), nhưng với CNN lại cần ít hơn số parameter từ filter map và số lượng parameter này có thể được chúng ta định lượng.

Pooling layer

Thường giữa các lớp Convolutional Layer với nhau người ta sẽ chèn vào 1 lớp Pooling layer để giảm bớt số lượng parameter lại nếu như đầu vào quá lớn. Có nhiều loại pooling layer, nhưng mình chỉ giới thiệu max pooling.

 

 Ví dụ ở trên, lớp max pooling có kích thước là 2*2, stride = 2. Với mỗi lần áp lên input, nó sẽ lấy giá trị lớn nhất trong khoảng filter đó và để nó vào output.

ReLU layer

Khái niệm về ReLU mình đã nói trong bài này rồi, các bạn quay lại để xem nhá. Thường thì sau khi feature map được tính ra, người ta sẽ xếp theo sau đó 1 lớp ReLU, lớp này sẽ áp dụng hàm ReLU lên tất cả các giá trị của feature map.

Fully Connected Layer

Để đưa ra được kết quả dự đoán thì lớp Neural network sẽ được thêm vào sau một mang CNN. Lớp neural này cũng chỉ là ANN bình thường thôi chứ ko khác gì cả. Vậy một mạng CNN thông thường sẽ có cấu trúc các lớp như thế nào? Sau đây là ví dụ:

INPUT -> [[CONV -> RELU]*N -> POOL?]*M -> [FC -> RELU]*K -> FC

Read More

Cấu trúc của 1 neural

Mỗi neural sẽ nhận vào các input. Các input này có thể là giá trị của tập dataset đưa vào (ví dụ như các điểm ảnh), hoặc input này cũng có thể là các giá trị output của layer trước đó. Mỗi input đi vào sẽ kèm với 1 giá trị Weight. Weight này có thể hiểu là 1 cái cầu nối giữa input và neural.
Lấy ví dụ như cái mạng nhện trong nhà bạn ấy, nhà bạn nào sạch quá ko có mạng nhện thì qua nhà hàng xóm xin coi cái mạng nhện như nào. Những cái weight này giống như mấy đường nối của mạng nhện, còn mấy cái điểm giao của mạng nhện cũng như là neural. Ok chưa?. (thực ra chả liên quan gì đâu :/ ).
Nói vòng vo nãy h, vậy cuối cùng neural là gì, có nhiệm vụ làm gì? Các bạn cứ hiểu neural là cái phòng để tính toán xử lí các dữ liệu dựa vào input và weight. Ở đây, nó sẽ làm phép tính tổng của các tích WiXi (Trong đó Wi là weight, và Xi là input). Nghe quen không? Nó y chang như cái hàm linear classifier trong bài function score đấy.

$F = Wx .$

Sau khi qua căn phòng tính toán. Giá trị sẽ được đi qua 1 hàm transfer function ( hay Activation function). Hàm này sẽ tiếp tục xử lý tùm lum tá lả để đưa ra 1 giá trị output. Vậy hàm activation function này là gì?

Activation function:

Thực ra activation function là một hàm toán học thôi, định nghĩa vậy là dễ hiểu nhất. Có rất nhiều loại Activation function nhé, sau đây mình sẽ giới thiệu qua một số hàm activation function chính, và mình cũng giới thiệu công thức thôi. Còn mấy vụ giải thích mặt toán học để xem xét nó xịn chỗ nào, nó cùi chỗ nào thì mình sẽ ko bàn tới nhé.  
Sigmoid: Hàm này có công thức:

$\sigma (x)= \frac{1}{1+e^{-x}}$

Giá trị x sau khi đi vào hàm này sẽ cho kết quả là 1 giá trị trong khoảng 0 – 1.

Tanh:

$tanh(x)=2\sigma (2x)-1$

Hàm này sẽ cho ra giá trị trong khoảng -1 đến 1

 

ReLU:

$f(x)=max(0,x)$

Hàm này lấy giá trị của x nếu x>0. Nếu x<0 0.

Ngoài ra còn có rất nhiều hàm activation function khác mà mình sẽ không kể đến. Mỗi hàm sẽ có ưu nhược điểm riêng, tùy theo bài toán giải quyết mà người ta sẽ lựa chọn cho phù hợp.

Read More

Kiến trúc mạng neural nhân tạo

Kiến trúc của một mạng neural

Mạng neural nhân tạo, Aritificial Neural network (viết tắt là ANN). Đây là mạng đang được nhắc đến siêu nhiều trong các bài quảng cáo về công nghệ AI, bạn chắc hẳn đã gặp đâu đó những câu từ như: “chúng được xây dựng dựa trên công nghệ AI, công nghệ này áp dụng một mạng nơ ron nhân tạo để học dữ liệu.. bla bla”. Vậy rút cuộc cái ANN là gì? Dưới đây là một mô hình tổng quan ANN.

Một ANN có 3 thành phần :
Input layer: là lớp đầu vào, như mô hình trên thì lớp đầu vào nhận 3 giá trị.
Hidden layer: lớp ẩn. Lớp này nhận giá trị từ lớp liền kề trước. Sau đó xử lí các thứ các thứ rồi truyền tiếp đi lớp sau (Xử lí gì thì chúng ta sẽ tìm hiểu sau, giờ cứ hiểu vậy đã). Một mạng ANN có thể có nhiều hidden layer.
Output layer: lớp đầu ra, là cái lớp xuất ra giá trị sau khi tính toán .

Các khái niệm cơ bản:

Neural: Mỗi cái cục tròn tròn trong hình là 1 neural. Cục này có nhiệm vụ xử lý nhân cộng các giá trị rồi đưa ra kết quả. Cục neural này sẽ được giới thiệu trong bài này.  
Cách đếm số lớp của ANN: Khi đếm số lớp của ANN, chúng ta không đếm lớp input. Ví dụ mạng bên trái là 2 lớp, mạng bên phải là 3 lớp.  
Số lượng neural của mạng: số lượng neural được tính bằng tổng số neural của hidden layer và output layer. Ví dụ mạng bên trái là 6 neurals, còn mạng bên phải là 9 neurals.  
Số lượng parameters của mạng: cái này thì tùy vào bạn có muốn gộp chung Weight và bias hay không. Số lượng bias bằng số lượng neural. Số lượng weights bằng số lượng gạch nối. Mình thì sẽ tính số lượng parameter bằng tổng số weight và bias. Ví dụ mạng bên trái là 20 parameters ( không tính bias) và bên phải là 32 parameters (không tính bias).  
Fully connected Layer: là loại layer mà tất cả các neural của layer trước liên kết với tất cả neural của layer kế nó. Ví dụ cả 2 mạng trên đều là fully connected Layer.

Read More

Giải thích quá trình máy học

Sau quá trình học được score function, loss function, optimization (gradient descent), backpropagation. Mình sẽ giải thích cho mọi người quá trình máy học dựa trên những khái niệm này.

 Đầu tiên, một bức ảnh sẽ được đưa vào model dự đoán của chúng ta. Model ở đây thực chất là tập hợp các Weight và bias. Khi model này nhận input là bức ảnh, nó sẽ tính toán dựa theo Score function và đưa ra được kết quả dự đoán. Kết quả dự đoán này sẽ được so sánh với kết quả thực để tính ra được độ lỗi theo loss function. Toàn bộ quá trình này là quá trình forward.
 Tiếp đến, quá trình backpropagation bắt đầu. Khởi động quá trình tính đạo hàm riêng điên loạn cho toàn bộ W và b trong model. Sau khi tính được đạo hàm riêng, gradient descent sẽ được áp vào để cập nhật các W và b. Và vòng lặp thứ nhất kết thúc.
Vòng lặp thứ 2 bắt đầu! Bức ảnh lại được đưa vào, model lại tiếp tục tính toán theo score function. Nhưng vì ở vòng lặp thứ nhất, các W và b đã được cập nhật theo gradient descent, do đó ở lần lặp này, loss function được tính ra sẽ thấp hơn loss function ở lần lặp trước. Điều này đánh dấu cho một sự kiện quan trọng của học máy: qua quá trình lặp, kết quả dự đoán đã chính xác hơn. Tiếp đến sẽ lại là quá trình backpropagation và cập nhật model. Quá trình này lặp cho đến khi nào loss đủ nhỏ mà người dùng ưng ý thì sẽ dừng hoặc sẽ dừng sau 1 số hữu hạn vòng lặp đã được lập trình.
Và đó, tất cả quá trình lặp forward và backpropagation đó, là quá trình máy học. Quá đơn giản đúng không nào!

Read More

Backpropagation

Phần backpropagation này rất nặng về toán đạo hàm nhé. Nên ai chưa có kiến thức đạo hàm riêng thì bắt buộc phải học trước đi nhé.

Ý nghĩa của đạo hàm riêng

Giả sử ta có hàm f = xy. Theo đạo hàm riêng thì ta có:

$\frac{\delta f}{\delta x}=y$ , $\frac{\delta f}{\delta y}=x$

Ví dụ với x= 4 và y =-3. Quá trình forward là quá trình tính toán theo biểu thức để ra kết quả. Tức forward ở đây là 4.-3 = -12. Lúc này, ta có đạo hàm riêng theo x = -3. Điều này có nghĩa là, nếu ta tăng giá trị của x 1 khoảng h nào đó, thì toàn bộ hàm f sẽ giảm một khoảng là -3h. Tương tự với đạo hàm riêng theo y = 4. Điều này có nghĩa, nếu ta tăng giá trị y 1 khoảng h nào đó, thì toàn bộ giá trị của f sẽ tăng 1 khoảng 4h. Như vậy, có thể hiểu:

Đạo hàm riêng của 1 biến chỉ ra được sự ảnh hướng của biến đó tới sự biến động của toàn bộ hàm số.

Các ví dụ

Giả sử ta có biểu thức: f(x,y,z)=(x+y)z. Giả sử x = -2, y = 5, z = -4. Ta có thể vẽ biểu thức như sau:

Còn quá trình backpropagation là quá trình tính đạo hàm của từng thành phần bằng cách tính ngược từ kết quả lên. Có thể thấy: q = x+ y có đạo hàm riêng là -4. Do đó, ta có thể nói rằng: nếu x hay y tăng thì q sẽ tăng, và f sẽ giảm 1 khoảng 4 lần giá trị tăng.  
Ví dụ tiếp theo cho hàm sigmoid Giả sử ta có hàm sau (gọi là hàm sigmoid):

$f(x,y)=\frac{1}{1+e^{-(w_{0}x_{0}+w_{1}x_{1}+w_{2})}}$

Ta có thể biểu diễn nó ra được như hình sau:

Quá trình tính toán forward cực kì đơn giản, bạn có thể tự tính ra được như trong hình. Mình sẽ giải thích quá trình backpropagation cho trường hợp này:
Giả sử cho kết quả output có đạo hàm = 1 cho dễ tính. Ta backward 1 bước về phép tính 1/x. Đạo hàm riêng của 1/x = -1/x^2 . Do đó ta có kết quả đạo hàm riêng tại đây là : (-1/1.37^2)*1 = -0.53. Tiếp đến ta backward 1 bước về phép tính x +1 . Đạo hàm theo x = 1. Do đó kết quả đạo hàm riêng tại đây = 1*-0.53 = -0.53. Tiếp tục backward lại 1 bước về phép tính :e^x . Ta có đạo hàm theo x của e^x = e^x. Do đó, đạo hàm riêng của x tại đây = e^-1*-0.53 = -0.2. Cứ thế, ta tính ngược cho đến input. Quá trình này chính là quá trình backpropagation.

Backpropagation và gradient descent

Quay lại với hàm score function, ta có $f(x_{i},W)=Wx_{i}$, loss function(SVM loss) $L_{i}=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+\Delta )$. Giả sử W là tập hợp của 1 trăm triệu weight từ W1 đến W100 triệu. Và qua quá trình backpropagation của hàm L, ta có đạo hàm riêng của $\frac{\delta L}{\delta W_{69}}=-4$. Điều này có ý nghĩa là: Nếu W69 tăng 1 khoảng h, thì L sẽ giảm 1 khoảng -4h. Đúng chưa nào? Mục tiêu chúng ta đặt ra từ đầu là làm cho L giảm (loss càng thấp thì dự đoán càng chính xác).
Tiếp tục ôn bài gradient descent nè: để L giảm thì ta xài gradient descent với công thức $W_{t+1} = W_{t}-\alpha f'(W_{t})$. Với $\alpha > 0$. Áp vào cho W69, ta có : $W'_{69} = W_{69} - \alpha(-4)$. Tức là W69 sẽ tăng sau vòng lặp này, đồng nghĩa là L sẽ giảm sau vòng lặp này.
 Và bây giờ, hiệu ứng quá rõ ràng: nhờ backpropagation tính ra đạo hàm riêng cho W, mà ở bước lặp tiếp theo, W sẽ thay đổi dựa vào gradient descent. Và sự thay đổi này làm L ở vòng lặp tiếp theo giảm. Tức là sự dự đoán ở vòng lặp tiếp theo sẽ chính xác hơn!

Read More

L2 Regularization

Trong máy học, vấn đề nhức nhối bao nhiêu con người ưu tú của nhân loại là Overfitting, do đó, có rất nhiều người đêm quên ăn, ngày ăn bù để suy nghĩ làm sao để hạn chế được Overfitting. Và một ý tưởng chợt lóe ra, ý tưởng này có thể mường tượng được như sau: bạn có một model với tập hợp các parameters, parameters càng nhiều thì model càng phức tạp. Đúng chưa? mà model càng phức tạp thì overfitting càng dễ gặp. Vậy để giảm overfitting, ta cần giảm độ phức tạp model, để giảm độ phức tạp model, ta giảm số lượng parameters. Mà để giảm số lượng parameters thì ta làm sao? Ta phải cho các parameters có giá trị càng gần 0 càng tốt. Vì sao? Vì nếu càng gần 0, thì sức ảnh hưởng của parameters càng ít và gần như tiêu biến. Và đó, là cách giảm parameters.
Ý tưởng đã có, vậy làm thế nào để giảm được giá trị của W mà độ chính xác của model vẫn ngon lành. Đây là lúc L2 Regularization có tác dụng. Ví dụ với hàm Linear Classifier, ta có hàm tổng quan là :

$f(x_{i},W)=Wx_{i}$

Giả sử ta có input x = [1,1,1,1], ta có 2 W lần lượt là W1 = [1,0,0,0] và W2 = [0.25,0.25,0.25,0.25]. Cả 2 đều cho ra cùng kết quả là 1. Và vì chung kết quả từ score function nên loss function SVM cũng tính ra chung 1 kết quả theo công thức:

$L_{i}=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+\Delta )$

Nhưng các bạn thấy, rõ ràng ở W2, các giá trị gần 0 hơn, do đó sẽ giảm được overfitting. Vậy nên người ta đã nghĩ ra cách kết hợp hàm L2 Norm có công thức như sau:

$R(W)=\sum_{k}\sum_{l}W_{k,l}^{2}$

Nhìn công thức hầm hố vậy thôi, thực ra chỉ là tổng bình phương các giá trị của W. Kết hợp với SVM loss ta có:

$L_{i}=\sum_{j\neq y_{i}}max(0,s_{j}-s_{y_{i}}+\Delta )+\lambda \sum_{k}\sum_{l}W_{k,l}^{2}$

Ta có R(W1)=1, R(W2)=0.25. Vậy nên, L2 < L1. Do đó, với hàm loss này, ta sẽ chọn L2, chính là chọn W2. Và đó, đó chính là cách L2 Regularization được áp dụng để hạn chế overfitting. Với việc lập trình, mình thấy người ta hay dùng thuật ngữ Weight decay, và weight decay cũng chính là L2 Regularization.

Read More